Le principe général d’un intervalle de confiance consiste à déterminer, à partir de ce qui a été observé dans un sous-échantillon, un intervalle dans lequel la grandeur que l’on étudie, au sein de la population dont est extrait l’échantillon, a de fortes chances de se situer. En l’occurrence, il s’agit de déterminer un intervalle, connaissant la proportion p observée dans l’échantillon, au sein duquel la proportion π réelle de la population étudiée se situe avec une probabilité égale à une valeur fixée à l’avance, usuellement 95 %, et notée 1-α.

Il s’agit donc de rechercher a et b tels que p[a ≤ π ≤ b]=1-α. α correspond au risque d’erreur que nous acceptons de prendre. Nous pouvons interpréter cet intervalle de confiance par “il y a une probabilité de 1-α pour que π soit compris entre a et b”.

Dans la suite de notre propos, nous nous situerons dans le cadre d’un échantillonnage aléatoire simple issu d’une population infinie. Dans les faits, les populations que nous étudions ne sont pas infinies mais sont suffisamment grandes comparées à la taille de nos échantillons (le plus souvent, il s’agit de populations de plusieurs millions d’individus tandis que nos enquêtes portent sur quelques milliers de personnes au plus) pour que nous puissions considérer qu’il s’agit d’une population infinie. Des corrections sont techniquement possibles. En l’espèce, nous pouvons négliger cet aspect.

Loi Binomiale

Nous noterons n la taille de notre échantillon. Le nombre d’individus observés, parmi les n enquêtés, présentant le caractère étudié est donc égale à np. Ce nombre np suit ce que l’on nomme une loi Binomiale de paramètre n et π. Il s’agit d’une loi discrète et non continue. En effet, np ne peut être qu’un nombre entier. Si 100 personnes ont été enquêtées, 12 ou encore 58 parmi elles peuvent présenter un caractère donné, mais cela ne peut être 12,5 ou 58,3. Le caractère discret de la loi binomiale implique que le calcul d’un intervalle de confiance exact est relativement compliqué et il a amené à de vives discussions parmi les statisticiens sur la manière adéquate de procéder ( [Clopper 1934], [Cassignol 1954], [Dumas 1955], [Vessereau 1978], [Brenner 1990], [Copas 1992]).

Cependant, dès lors que l’échantillon est suffisamment grand, il est possible d’avoir recours au théorème central limite qui permet de simplifier le calcul, p pouvant être alors approximé par une loi Normale.

De plus, dans le cadre d’un tirage aléatoire simple avec remise (ce qui correspond à une population-mère infinie), nous pouvons considérer que la sélection de chaque individu de l’échantillon est indépendante des autres individus sélectionnés. Il en résulte alors que le meilleur estimateur possible de la proportion réelle π est la proportion observée p. D’un point de vue plus formel, p est un estimateur sans biais, efficace et convergent de π et correspond à l’estimateur obtenu par la méthode du maximum de vraisemblance ( [Bouzitat 1990], p. 164, 166, 169 et 175).

Plusieurs méthodes ont été développées pour calculer l’intervalle de confiance d’une proportion. Nous ne présenterons ici que quatre d’entre elles :

• la méthode standard traditionnelle, nommée méthode asymptotique ou bien encore méthode WALD par VOLLSET ( [Vollset 1993]) et d’autres auteurs à sa suite ;
• la méthode de score ou méthode WILSON ( [WILSON 1927]), encore appelée méthode de l’ellipse ;
• la méthode WALD avec correction de continuité ( [Blyth 1983]) ;
• la méthode de score de WILSON avec correction de continuité ( [Gosh 1979], [Vollset 1993]).

Un calculateur en ligne pour ces quatre méthodes est disponible à l’adresse suivante : http://www.ac-poitiers.fr/math/prof/resso/cali/ic_phrek.html. Ces quatre méthodes sont également disponibles dans la feuille de calcul jointe.

Des méthodes plus complexes ont également été proposées mais elles sont plus difficiles à mettre en œuvre. Par ailleurs, le gain apporté à les utiliser est le plus souvent limité dans le cadre d’un usage courant.

Méthode standard (Wald)

Selon le théorème central limite, la moyenne expérimentale d’une répétition d’expériences identiques converge, quand n augmente, vers une loi Normale. Il en résulte que, pour n suffisamment grand, nous pouvons considérer que p suit une loi Normale de moyenne π et d’écart-type . Usuellement, on considère que cette approximation est valable pour n supérieur à 30 ( [Jolion 2006], p. III-8). D’autres auteurs préconisent que l’on ait observé au moins 5 succès et 5 échecs : soit np≥5 et n(1-p)≥5 ( [Wonnacott 1990], p. 310).

La différence p-π suit donc une loi Normale de moyenne nulle et de même écart-type. Comme π est inconnue, nous ne connaissons pas la valeur exacte de l’écart-type. Il existe deux possibilités pour l’approximer. On utilise le majorant (c’est-à-dire la plus grande valeur possible) de π(1-π) à savoir ¼. Ou bien, on remplace π par son estimation p pour le calcul de l’écart-type, ce qui est la méthode la plus courante.

Si l’on note z la valeur pour laquelle la fonction de répartition de la loi Normale centrée réduite est égale à 1-α/2, les bornes de l’intervalle de confiance de π sont alors égales à :

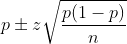
Cette méthode est la plus courante. Si elle produit des intervalles de confiance parfaitement centrés autour de la proportion observée, elle peut induire, pour des valeurs de p proches de 0 ou de 1, des intervalles dont une partie est inférieure à 0 ou supérieure à 1. Il est alors nécessaire de tronquer l’intervalle pour supprimer les valeurs aberrantes. Cette approximation n’est donc valable que pour une valeur de p proche de 50%.

Méthode de score (Wilson)

Comme pour la méthode standard, la méthode de score utilise la convergence de la loi Binomiale vers la loi Normale et approxime l’écart type en remplaçant π par p. Cette approche suggère que l’on peut obtenir un intervalle de confiance en prenant en compte les valeurs de π telles que :

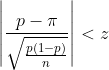
En élevant cette inégalité au carré puis en résolvant l’équation au second degré obtenue, on détermine alors les bornes de l’intervalle de confiance par la formule :

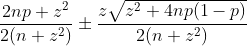
Cet intervalle de confiance n’est plus centré sur p et présente l’avantage de ne pas produire de valeur aberrante (inférieure à 0 ou supérieure à 1).

Pour plus de détails sur la résolution de l’équation, voir le mémoire de Patrick GAGNON ( [Gagnon 2006], p. 12-13).

Correction de continuité

Il s’agit d’une correction, initialement proposée par YATES [Yates 1934], pour tenir compte du passage d’une loi discrète à une loi continue. Chaque nombre entier x sera considéré comme couvrant l’intervalle allant de x-½ à x+½. Cela induit une légère modification des formules pour le calcul des intervalles de confiance. Pour la méthode de WALD on obtient ainsi :

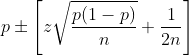
et pour la méthode de WILSON :

Choix d’une méthode

Différents auteurs ont comparé l’efficacité de plusieurs méthodes, dont les quatre présentées ici, ainsi que des méthodes de calcul plus complexes ( [Newcombe 1998], [Tobi 2005], [Tsai 2007]). Si la méthode classique doit être évitée parce qu’il s’agit de la moins performante et qu’elle produit des valeurs aberrantes, la méthode WILSON de score avec correction de continuité est recommandée dans la mesure où ses performances sont presque équivalentes à celles de méthodes dites exactes et où son calcul est relativement aisé.

Valeurs courantes de z

Nous avons noté z la valeur pour laquelle la fonction de répartition de la loi Normale centrée réduite est égale à 1-α/2. Le plus souvent, les intervalles de confiance calculés sont les intervalles à 95%, parfois 90% et plus rarement 99%.

Voici les valeurs de z correspondantes pour ces cas les plus fréquents :

• intervalle de confiance à 90 % : z= 1,64485362695 ≈ 1,645
• intervalle de confiance à 95 % : z= 1,95996398454 ≈ 1,960
• intervalle de confiance à 99 % : z= 2,57582930355 ≈ 2,576

Notes :

[Clopper 1934] CLOPPER C. J. et PEARSON E. S., « The Use of Confidence or Fiducial Limits Illustrated in the Case of the Binomial », Biometrika, n°26(4), 1934, pages 404-413.

[Cassignol 1954] CASSIGNOL C., « Note sur la construction d’intervalles de confiance pour la proportion de défectueux d’un lot à partir d’échantillons d’effectifs peu élevés », Revue de statistique appliquée, n°2(3), 1954, pages 43-55. (http://www.numdam.org/item ?id=RSA_1954__2_3_43_0)

[Dumas 1955] DUMAS M., « Choix et détermination pratique d’intervalles de confiance », Revue de statistique appliquée, n°3(3), 1955, pages 85-101. (http://www.numdam.org/item ?id=RSA_1955__3_3_85_0)

[Vessereau 1978] VESSEREAU A., « Sur l’intervalle de confiance d’une proportion logique « classique » et logique « bayesienne » », Revue de statistique appliquée, n°26(2), 1978, pages 5-31. (http://www.numdam.org/item ?id=RSA_1978__26_2_5_0)

[Brenner 1990] BRENNER D. J. et QUAN H., « Exact Confidence Limits for Binomial Proportions-Pearson and Hartley Revisited », The Statistician, n°39(4), 1990, pages 391-397.

[Copas 1992] COPAS J. B., « Exact Confidence Limits for Binomial Proportions-Brenner & Quan Revisited », The Statistician, n°41(5), 1992, pages 569-572.

[Bouzitat 1990] BOUZITAT C., BOUZITAT P. et PAGÈS G., Statistique, Probabilités, Estimation ponctuelle : cours et exercice d’application, Cujas, Paris (FR), 1990, 224 pages.

[Vollset 1993] VOLLSET S. E., « Confidence intervals for a binomial proportion », Statistics in Medicine, n°12(9), 1993, pages 809-824.

[WILSON 1927] WILSON E. B., « Probable inference, the law of succession, and statiscal inference », Journal of the American Statistical Association, n°22, 1927, pages 209-212.

[Blyth 1983] BLYTH C. R. et STILL H. A., « Binomial confidence intervals », Journal of the American Statistical Association, n°78, 1983, pages 108-116.

[Gosh 1979] GOSH B. K., « A comparison of some approximate confidence intervals for the binomial parameter », Journal of the American Statistical Association, n°74, 1979, pages 894-900.

[Jolion 2006] JOLION J.-M., Probabilités et Statistique - Cours de troisième année, Lyon (FR), INSA, Département génie Industriel, 2006, 120 pages. (http://rfv.insa-lyon.fr/ jolion/PS/poly_stat.pdf)

[Wonnacott 1990] WONNACOTT T. H. et WONNACOTT R. J., Statistique : économie - gestion - sciences – médecine, Economica, réimpression de 1995 de la traduction française de 1991 à partir de la quatrième édition américaine de 1990, 1972 pour la première édition originale, Paris (FR), 1990, 920 pages.

[Gagnon 2006] GAGNON P., Intervalles de confiance pour une différence de deux proportions, mémoire pour l’obtention du grade de Maître ès Sciences (M. Sc.), sous la direction de BÉLISLE C., Université de Laval, Faculté des Sciences et de Génie, Québec (CA), 2006, 94 pages. (http://www.theses.ulaval.ca/2006/24060/24060.pdf)

[Yates 1934] YATES F., « Contingency table involving small numbers and the Khi² test », Supplement to the Journal of the Royal Statistical Society, n°1(2), 1934, pages 217-235.

[Newcombe 1998] NEWCOMBE R. G., « Two-sided confidence intervals for the single proportion : comparison of seven methods », Statistics in Medicine, n°17(8), 1998, pages 857-872.

[Tobi 2005] TOBI H., VAN DEN BERG P. B. et DE JONG-VAN DEN BERG L. T., « Small proportions : what to report for confidence intervals ? », Pharmacoepidemiology and drug safety, n°14(4), 2005, pages 239-247.

[Tsai 2007] TSAI W. Y., CHI Y. et CHEN C. M., « Interval estimation of binomial proportion in clinical trials with a two-stage design », Statistics in Medicine, n°27(1), 2007, pages 15-35, DOI : 10.1002/sim.2930.